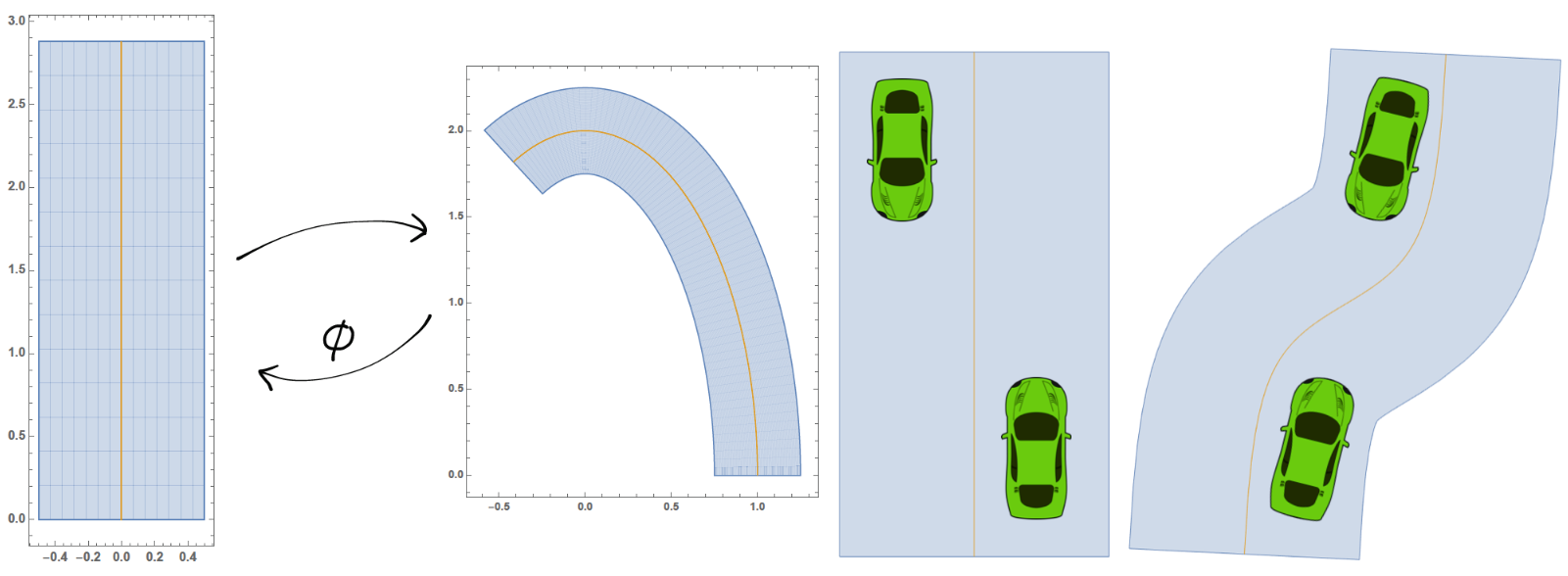
In 2017, Shalev-Schwartz, Shammah and Shashua published an article on the preprint server arXiv entitled «On a Formal Model of Safe and Scalable Self-driving Cars». In this paper, a deterministic safety model called RSS is introduced and the article claims that if every road user adheres to the rules given by RSS, then no accidents can happen. The goal of this project was to inspect the article and to either validate the model or to find counterexamples to the claims made therein. Although the approach presented in the article seems promising, we were able to find shortcomings of the work by constructing scenarios in which RSS does not provide a guarantee for no accidents. Furthermore, we detected lines of thought along which the model could be refined.
Joint work with Corinne Hager Jörin and Florence Yerly.
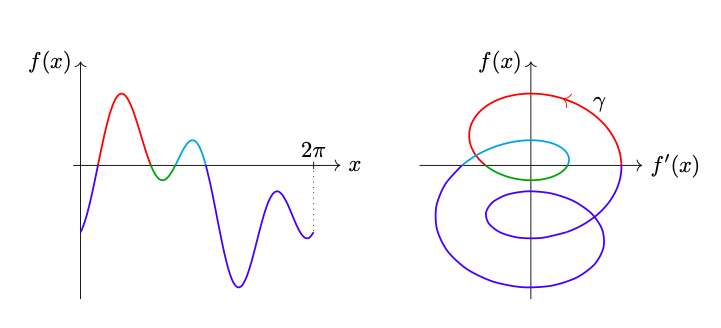
A basic task in mathematics or mathematical modelling consists in solving equations. Since it is often times impossible to solve equations analytically, one is interested in understanding properties of the solution space of the equation, e.g. its cardinality. In this work we construct a method that allows to count the number of solutions of a real equation in one real variable without solving the equation. Based on geometric ideas, we construct an integral that counts the number of solutions to an equation under mild regularity assumptions.
N. Hungerbühler, M. Wasem, An integral that counts the zeros of a function, Open Math, 2018
Absolute and relative change might be insufficient to meaningfully compare and interpret the sales volume of different sales channels. The goal of this project was to single out a meaningful indicator which is determined by some economically natural axioms and which allows to compare sales channels of different scales. The indicator proves to be interesting in its own right since it uncovers a relationship between marginal functions and economic elasticity and might be interpreted as a special kind of Cobb-Douglas-Function.
Mathematics at your service
mathematical modelling, econometrics, differential geometry